相似距离算法是推荐算法的一部分。
一、EuclideanDistanceSimilarity: 欧氏距离相似度
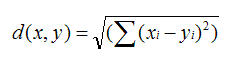
原理:利用欧式距离d定义的相似度s,s=1 / (1+d)。
范围:[0,1],值越大,说明d越小,也就是距离越近,则相似度越大。
说明:同皮尔森相似度一样,该相似度也没有考虑重叠数对结果的影响,同样地,Mahout通过增加一个枚举类型(Weighting)的参数来使得重叠数也成为计算相似度的影响因子。
二、PearsonCorrelationSimilarity: 皮尔森相似度
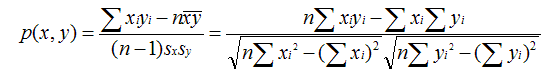
原理:用来反映两个变量线性相关程度的统计量
范围:[-1,1],绝对值越大,说明相关性越强,负相关对于推荐的意义小。
说明:1、 不考虑重叠的数量;2、 如果只有一项重叠,无法计算相似性(计算过程被除数有n-1);3、 如果重叠的值都相等,也无法计算相似性(标准差为0,做除数)。
该相似度并不是最好的选择,也不是最坏的选择,只是因为其容易理解,在早期研究中经常被提起。使用Pearson线性相关系数必须假设数据是成对地从正态分布中取得的,并且数据至少在逻辑范畴内必须是等间距的数据。Mahout中,为皮尔森相关计算提供了一个扩展,通过增加一个枚举类型(Weighting)的参数来使得重叠数也成为计算相似度的影响因子。
三、UncenteredCosineSimilarity: 余弦相似度
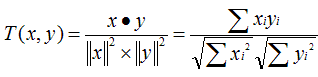
原理:多维空间两点与所设定的点形成夹角的余弦值。
范围:[-1,1],值越大,说明夹角越大,两点相距就越远,相似度就越小。
说明:在数学表达中,如果对两个项的属性进行了数据中心化,计算出来的余弦相似度和皮尔森相似度是一样的,在mahout中,实现了数据中心化的过程,所以皮尔森相似度值也是数据中心化后的余弦相似度。另外在新版本中,Mahout提供了UncenteredCosineSimilarity类作为计算非中心化数据的余弦相似度。
四、SpearmanCorrelationSimilarity: Spearman秩相关系数相似度
原理:Spearman秩相关系数通常被认为是排列后的变量之间的Pearson线性相关系数。
范围:{-1.0,1.0},当一致时为1.0,不一致时为-1.0。
说明:计算非常慢,有大量排序。针对推荐系统中的数据集来讲,用Spearman秩相关系数作为相似度量是不合适的。
五、CityBlockSimilarity: 曼哈顿距离相似度
原理:曼哈顿距离的实现,同欧式距离相似,都是用于多维数据空间距离的测度
范围:[0,1],同欧式距离一致,值越小,说明距离值越大,相似度越大。
说明:比欧式距离计算量少,性能相对高。
六、LogLikelihoodSimilarity: 对数似然相似度
原理:重叠的个数,不重叠的个数,都没有的个数
范围:具体可去百度文库中查找论文《Accurate Methods for the Statistics of Surprise and Coincidence》
说明:处理无打分的偏好数据,比Tanimoto系数的计算方法更为智能。
七、TanimotoCoefficientSimilarity: Tanimoto系数相似度
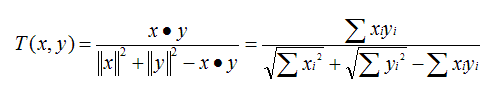
原理:又名广义Jaccard系数,是对Jaccard系数的扩展,等式为
范围:[0,1],完全重叠时为1,无重叠项时为0,越接近1说明越相似。
说明:处理无打分的偏好数据。